Στις 21 Μαρτίου συμμετείχαμε για πρώτη φορά στο πείραμα του Ερατοσθένη, μια διοργάνωση του εργαστηρίου καινοτομίας και του φόρουμ http://eratosthenes.ea.gr/. Οι μαθητές μας ενθουσιάστηκαν από τη διαδικασία και μέτρησαν με αρκετά μεγάλη ακρίβεια την ακτίνα της γης, με σημείο αναφοράς τον Ισημερινό.
Το Πείραμα του Ερατοσθένη
Θήβα 21 Μαρτίου 2014
12:34μ.μ
Πινδάρειο-2ο Γυμνάσιο Θήβας
Συντεταγμένες: 38°19’21″N 23°19’17″E
Πώς ?έτρησε ο Ερατοσθένης την περιφέρεια της γης
Ο Ερατοσθένης έζησε τον 3ο π.Χ. αιώνα στην Αλεξάνδρεια της Αιγύπτου την εποχή της
Μακεδονικής δυναστείας των Πτολε?αίων, που είναι γνωστή ως Ελληνιστική Εποχή.
?ιατέλεσε διευθυντής της φη?ισ?ένης Βιβλιοθήκης της Αλεξάνδρειας και άφησε πλούσιο
έργο στα ?αθη?ατικά, την αστρονο?ία, τη γεωγραφία και τη φιλοσοφία2,4.
Ο Ερατοσθένης οργάνωσε και πραγ?ατοποίησε ένα από τα πιο διάση?α, αλλά και ένα
από τα πιο ση?αντικά πειρά?ατα στην ιστορία των θετικών επιστη?ών, τη ?έτρηση της
περιφέρειας της γης ?ε έναν ιδιαίτερα ιδιοφυή τρόπο και ?ε αξιοζήλευτη για την εποχή του
ακρίβεια.
Ο Ερατοσθένης διάβασε σε έναν αρχαίο πάπυρο, στη βιβλιοθήκη της Αλεξάνδρειας, για
ένα πηγάδι κοντά στη Συήνη, στο οποίο το ?εση?έρι της 21ης Ιουνίου, θερινό ηλιοστάσιο, οι ακτίνες του Ήλιου έπεφταν κάθετα στη γη και φώτιζαν τον πάτο του, χωρίς να αφήνουν
κα?ία σκιά. Την ίδια στιγ?ή στην Αλεξάνδρεια, που βρίσκεται στον ίδιο ?εση?βρινό ?ε τη
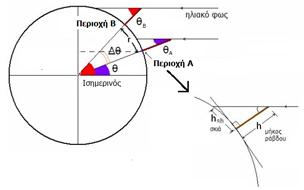
Συήνη, οι ακτίνες του ηλίου ?ε την κατακόρυφο του τόπου σχη?ατίζουν γωνία 7ο περίπου,όπως φαίνεται στο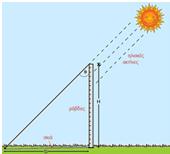 
σχή?α 1
Η γωνία Δθ είναι η γωνιάκη απόσταση μεταξύ των δυο περιοχών.
Στη συνέχεια μετράμε την απόσταση των δυο περιοχών πάνω στον ίδιο μεσημβρινό. γνωρίζοντας την γωνιακή και τη πραγματική απόσταση των δυο περιοχών με απλή μέθοδο των τριών, όπως και ο Ερατοσθένης υπολογίζουμε την περιφέρεια της Γης.
Έτσι ?πόρεσε να υπολογίσει την περιφέρεια της γης ?ε έναν κο?ψό τρόπο που προκαλεί
το θαυ?ασ?ό της επιστη?ονικής κοινότητας ακό?η και σή?ερα.
Πώς ?πορού?ε να επαναλάβου?ε τη ?έτρηση του Ερατοσθένη
Ο Ερατοσθένης πραγ?ατοποίησε τη ?έτρηση της περιφέρειας της γης το ?εση?έρι του
θερινού ηλιοστασίου. Για να επαναλάβου?ε την ?έτρηση του Ερατοσθένη ?ε τους ?αθητές
?ας, προφανώς θα θέλα?ε να ?πορού?ε να την επαναλάβου?ε ?ια οποιαδήποτε η?ερο?ηνία και να χρησι?οποιήσου?ε ως τόπο τη θέση του σχολείου ?ας. Επο?ένως, θα πρέπει να γίνουν ?ερικές τροποποιήσεις στη ?έθοδο του Ερατοσθένη που να ανταποκρίνονται στη διαφορετική η?ερο?ηνία που γίνεται το πείρα?α και στους διαφορετικούς τόπους που θα χρησι?οποιηθούν.
Το πρώτο βή?α που θα πρέπει να κάνου?ε είναι να επιλέξου?ε ?ια ?έρα ?ε ήλιο. Στη
συνέχεια θα πρέπει να υπολογίσου?ε την ώρα που ?εσουρανεί ο ήλιος στον τόπο ?ας. Ο
ήλιος δεν ?εσουρανεί σε ένα τόπο στις 12:00 το ?εση?έρι ?ιας και η ώρα Ελλάδος είναι η
ώρα του ?εση?βρινού που έχει γεωγραφικό ?ήκος 30ο
ανατολικό (+2 GTM). Ο πιο εύκολος τρόπος για να βρού?ε την ώρα που ?εσουρανεί ο ήλιος σε ένα τόπο είναι να χρησι?οποιήσου?ε την ένδειξη ενός ηλιακού ρολογιού. Όταν ένα ηλιακό ρολόι δείχνει 12:00 τότε ο ήλιος ?εσουρανεί στον τόπο.
Την ώρα που ?εσουρανεί ο ήλιος στον τόπο ?ας ?ετρού?ε τη γωνία που σχη?ατίζουν οι
ακτίνες του ηλίου ?ε την κατακόρυφο του τόπου. Για το σκοπό αυτό χρησι?οποιού?ε ?ια
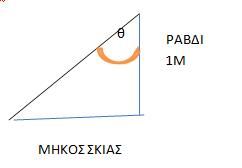
κατακόρυφο ράβδο γνωστού ?ήκους και ?ετρού?ε τη σκιά της. Υπολογίζου?ε την
εφαπτο?ένη της γωνίας όπως φαίνεται στο σχή?α 2.
Σχή?α 2. Η ?έτρηση της γωνίας που σχη?ατίζουν:
Εφθ= ΜΗΚΟΣ ΣΚΙΑΣ 
100cm
Στο σχολείο μας το πείραμα πραγματοποιήθηκε στις 21 Μαρτίου 2014 στις 12:34μ.μ και έδωσε τις ακόλουθες τιμές: μήκος σκιάς:78,6 cm , Μήκος ραβδιού 100 cm
Εφθ=7,86 και Θ=37,52426
37,52426/360=4243,64χμ/περιφέρεια της Γης
Περιφέρεια της Γης=4243,64χμ*360/37,52426 =40.712,6057 χμ
Συντονιστής πειράματος :Κυπραίου Σταυρούλα Ιωάννα
Συμμετείχαν: 42 Μαθητές και 5 εκπαιδευτικοί.